树

完全二叉树

概念

• 从上到下，从左到右放置，即为完全二叉树
• 除了最下层，中间层全满
• 最下层节点从左到右排列

满二叉树

概念

• 非叶子节点，都有两个子节点。即节点要么没孩子，要么有俩

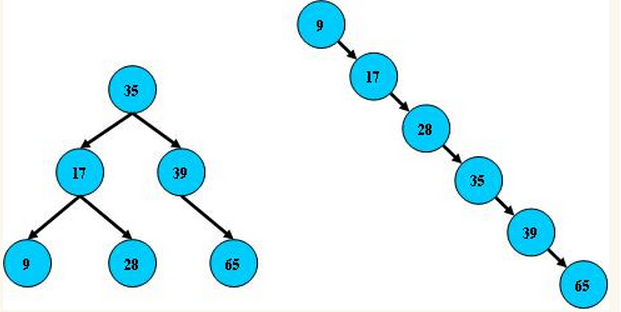
平衡二叉树

概念

• 基于二分法的树结构

特点：

• 非叶子节点最多存在两个子节点
• 每一个非叶子节点，左孩子值小于当前节点，右孩子值大于当前节点
• 没有重复值
• 左右子树高度相差不超过1（平衡性，实现方式有红黑树等，避免某一分支过高退化成链表）

B树

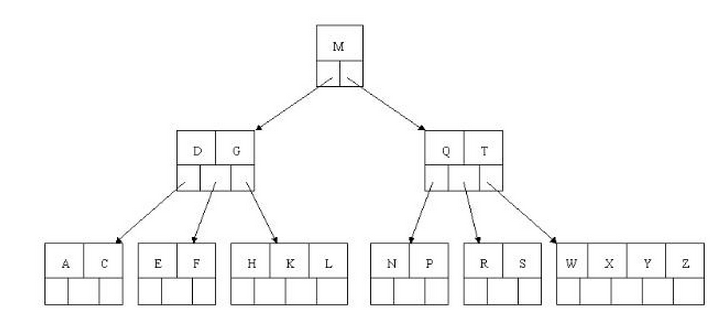
概念

• 平衡二叉树的改版，平衡多路查找树

特点

• 同平衡二叉树，左孩子值 < 当前节点值 < 右孩子节点值
• 每一层有两个数据，上层为关键字（同时有数据指针），下层为子节点指针
• 关键字数：>=ceil(M/2)-1, <=M-1
• M叉树：非叶节点的子节点数 >=2, <=M，M即查找路径
• 所有叶子节点都在同一层，包含关键字和数据或数据指针

插入过程

• M阶树，先组成一层M阶，超过后再向上拆分

删除

• 节点合并，先从子节点合，子节点没有满足条件则向父节点合

B+树

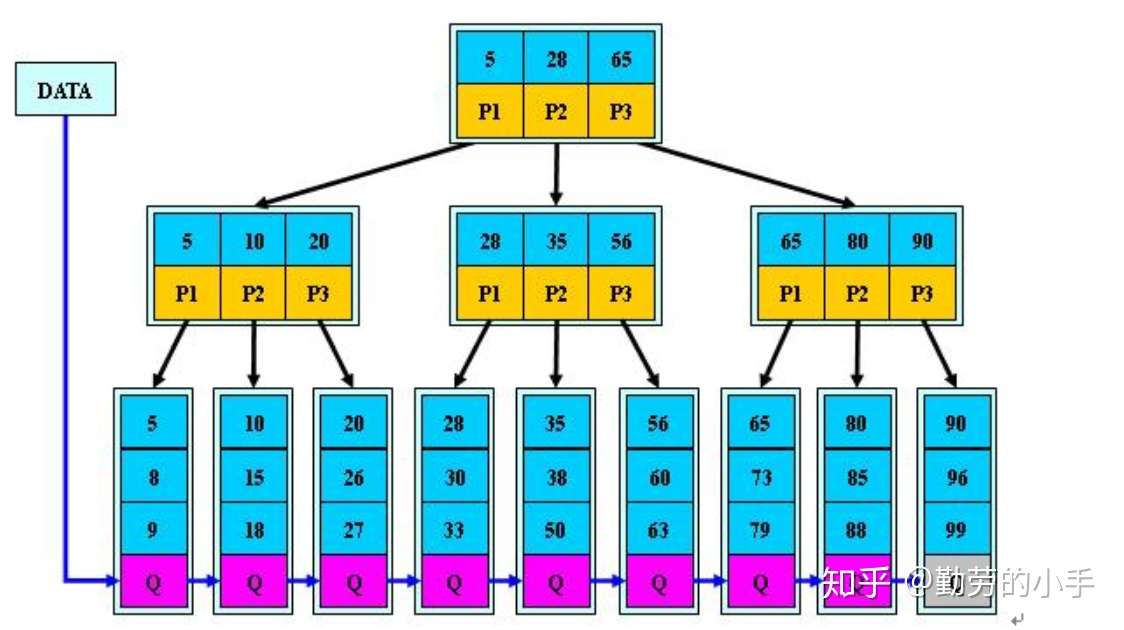
概念

• B树升级版

特点

• 非叶子节点不保存数据指针，只保存子节点索引
• 叶子节点保存父节点所有关键字的数据指针
• 叶子节点有序排列，上一叶子节点有指针指向下一叶子节点，成链表

优点

• 非叶子节点保存的索引更多，因而层级更少，查找速度更快
• 非叶子节点无数据指针，每次查询都必须查到叶子节点，因而速度差不多，即性能稳定
• 叶子节点可排序，天然具体排序功能，利于区间查找
• 同上，所以全节点遍历更快

堆

特点

• 偏序：
  • 大根堆：父节点值大于等于左右子节点
  • 小根堆：父节点值小于等于左右子节点
• 完全二叉树

堆存储

数组表示，对于第i个节点，若索引从0开始

• 父节点：(i - 1) / 2
• 左子节点：2 * i + 1
• 右子节点：2 * i + 2

堆向下调整

替换堆顶元素后，调整使堆重新满足性质
过程：

• 将根节点，与左右子树比较并视需要交换
• 接着交换直至不再需要交换

堆向上调整

在堆尾新加入一个元素，将堆节点循环与父节点比较，直至满足性质

建立堆

1、从最后一个非叶子节点开始，将其与左右子树比较并调整

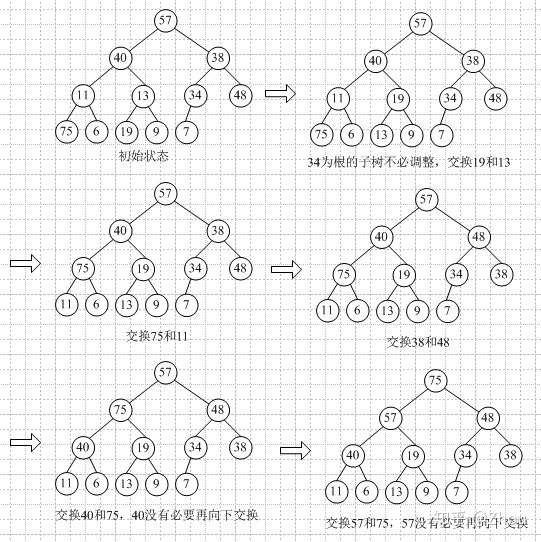
删除堆顶

将最后一个元素的值赋给堆顶，进行一次从上到下的调整

插入元素

插入到未尾，然后进行一次堆向上调整

堆排序

过程：

• 建立堆
• 将堆顶与最后元素交换，标记未尾区域为有序区，前面区域为无序区
• 堆由上到下调整
• 继续交换堆顶与无序区最后一个元素

package fighting.algorithm.sort;

import java.util.Arrays;

public class HeapSort {

    /**
     * 测试
     */
    public static void main(String[] args) {
        int[] arr = new int[]{22, 3, 44, 5, 12, 4, 67, 23, 11};
        System.out.println(Arrays.toString(arr));

        heapSort(arr);
        System.out.println(Arrays.toString(arr));
    }

    /**
     * 堆排序
     */
    public static void heapSort(int[] arr) {
        // 建立堆
        buildHeap2(arr);

        // 循环将堆顶与无序区最后一个元素交换，则无序区减1，有序区加1
        for (int lastUnsortIndex = arr.length - 1; lastUnsortIndex > 0; lastUnsortIndex--) {
            swap(arr, 0, lastUnsortIndex);
            heapAdjust(arr, 0, lastUnsortIndex);
        }
    }

    /**
     * 建立堆
     * 从最后一个非叶子节点开始，循环堆调整来建立堆
     *
     * @param arr 数组
     */
    public static void buildHeap(int[] arr) {
        for (int i = arr.length / 2 - 1; i >= 0; i--) {
            heapAdjust(arr, i, arr.length);
        }
    }

    /**
     * 建立堆
     * 循环取元素插入到堆中，直到元素取完
     *
     * @param arr 数组
     */
    public static void buildHeap2(int[] arr) {
        for (int i = 0; i < arr.length; i++) {
            siftUp(arr, i);
        }
    }


    /**
     * 堆向下调整
     * 
     * 将第i个节点及其子树，调整为一个堆
     *
     * @param arr 数组
     * @param i   待调整的元素
     * @param len 数组长度
     */
    public static void heapAdjust(int[] arr, int i, int len) {
        int child;
        while ((child = i * 2 + 1) < len) {
            if (child + 1 < len && arr[child] < arr[child + 1]) {
                child++;
            }
            if (arr[i] < arr[child]) {
                swap(arr, i, child);
                i = child;
            } else {
                break;
            }
        }
    }

    /**
     * 堆向上调整
     *
     * @param arr 数组
     * @param i   待调整的元素位置
     */
    public static void siftUp(int[] arr, int i) {
        int parent;
        while ((parent = (i - 1) / 2) >= 0) {
            if (arr[i] > arr[parent]) {
                swap(arr, i, parent);
                i = parent;
            } else {
                break;
            }
        }
    }

    public static void swap(int[] arr, int a, int b) {
        int tmp = arr[a];
        arr[a] = arr[b];
        arr[b] = tmp;
    }

}

字典树